El fomento de las matemáticas en la educación preescolar y en el jardín

Introducción

¿Cómo ayudar mejor a estudiantes a aprender el hecho que un solo digito (básico), en la sumatoria básica, como 3 + 4 = 7 y 9 + 5 = 15, y también en la sustracción, como 7 – 3 = 4 y 14 – 9= 5? Ha sido una temática de un largo debate. (Ver, por ejemplo., Baroody & Dowker,¹ particularmente los capítulos 2, 3, 6, y 7). Sin embargo, existe un consenso general sobre el hecho de que los niños y las niñas necesitan concretar su fluidez.² El hecho de la fluidez implica la realización de las sumas y las restas eficientemente eficientementey (con rapidez y flexibilidad) y aplicando este conocimiento de manera adecuada y flexible . En la últimas cuatro décadas, se ha ido despejando la idea de que las matemáticas es un conocimiento importante para los niños y las niñas todos los días (informal), como base del aprendizaje en la escuela (formal).^3,4,5 Por ejemplo, la investigación sustenta que el apoyar a los niños y las niñas a construir el sentido numérico puede promover la fluidez.^6,7,8,9 El hecho de esta aseveración, es resumir cómo el desarrollo del sentido numérico informal antes del primer grado, proporciona una base para la destreza formal clave de fluidez en los grados primarios.

Preguntas directrices

1. ¿Cuándo los padres y las madres, como profesores(as) de la primera infancia deben comenzar a promover (a) el proceso del sentido numérico y; (b) los esfuerzos para fomentar el hecho de la fluidez directamente?
2. ¿Cuáles son los requisitos previos para que los niños y las niñas preescolares y del jardín necesitan para lograr eficiente y eficazmente el hecho de la fluidez?
3. ¿Qué rol juega el lenguaje en el desarrollo de este fundamental conocimiento?
4. ¿Cómo los padres y las madres, como profesores(as) de la primera infancia pueden alentar con mayor eficiencia el sentido numérico y el hecho de la fluidez?

Resultados de recientes investigaciones

Pregunta 1. El proceso de apoyar a los niños y a las niñas a construir el sentido numérico es basado en el hecho de la fluidez, puede y debiera iniciarse en la edad preescolar. En recientes investigaciones se indica que los niños y las niñas comienzan la construcción del sentido numérico muy temprano, incluso entre los 18 y los 2 años pueden comenzar  aprendiendo el desarrollo de prerrequisitos para el hecho de la fluidez (por ejemplo, ver Baroody, Lai, & Mix,³ para revisar).

Los esfuerzos exitosos para promover el hecho de la fluidez, dependen de la seguridad que el niño o la niña desarrollen en la lectura y que no sea de forma apresurada. En este sentido, la investigación indica que hay importantes diferencias individuales en el sentido numérico; las que aparecen temprano y generalmente son a los dos o tres años de edad, y con frecuencia aumentan con la edad,^3,10 aunque es de considerar que no hay una reglas absolutas al respecto. Para muchos niños, es posible que igual con las adiciones más sencillas (n + 0 y n + 1), una tal formación no sea apropiada en el plan del desarrollo antes del final de la maternal o el comienzo del primer año escolar.¹¹ Para los niños con riesgo de fracaso en el plano escolar, sucede con frecuencia que igual con las sumas más simples estas no tengan ningún sentido antes del primero o del segundo año.¹²

Pregunta 2 y 3. En algunas investigaciones se indica que el lenguaje, en la forma de las primeras palabras de los números, tiene un rol clave en la construcción del sentido numérico (para una discusión detallada ver Baroody;³ Mix, Sandhofer, & Baroody¹³). Específicamente, se puede proporcionar una base para dos sustentos del temprano sentido numérico, nominadas como un concepto de un número cardinal (el número total de elementos en un conjunto) y la habilidad de reconocimiento verbal de los números,algunas veces es llamada (verbal) subitizing, como se muestra en la Figura 1. El reconocimiento verbal de los números,  supone reconocer de forma fiable y eficiente el número de ítems de elementos en pequeños conjuntos y las palabras de los números apropiadas. El uso de “uno, dos, tres” de acuerdo a los ejemplos vistos y otros, puede ayudar a niños y niñas de 2 y 3 años a construir un concepto más preciso de los números “intuitivos” uno, dos y tres, y una comprensión de la unidad, dualidad y la trinidad numérica.

• Viendo ••, DD, y  o o (ejemplos de pares), todo señalados por dos, los niños pequenos pueden reconocer que la apariencia de los objetos haciendo parte de colecciones, no tiene ninguna importancia; (la forma y el color no son pertinentes para el número). Ello les puede brindar un identificador (“dos”) por el concepto intuitivo de pluralidad (más de un objeto).
• El hecho de ver •, •••, D, DDD, , y (son contra ejemplos de pares) señalados como “no siendo dos” o el nombre de otro número, puede ayudarles a definir le limite del concepto de dos.

Las implicaciones de las instrucciones son clave para una comprensión básica de número cardinal, porque no es innata ni tampoco se despliegan automáticamente (cf. Dehaene¹⁵).^14,16  Los padres y las madres, como también profesores(as) preescolares, tienen una importante labor para proporcionar experiencias y atender las necesidades en la construcción de conceptos numéricos. Por su parte, también debieran aprovechar las experiencias cotidianas significativas, para promover que el niño o la niña sea capaz de nombrar pequeñas colecciones (por ejemplo. “¿cuántos pies tienes? entonces necesitas dos zapatos”, “puedes tomar una galleta, no dos galletas”). Algunos niños y niñas entran al jardín sin ser capaces de reconocer intuitivamente los números, lo que implica que están en grave riesgo para fracasar en la escuela y necesitan trabajos de reparación intensiva. En el jardín, se debiera detectar de inmediato esta capacidad y comprobar si los niños y las niñas reconocen conjuntos de 1 a 3 objetos y si pueden distinguir de otros más grandes  de 4 o 5.

Tal como, lo ilustra la Figure 1, la co-evolución de los conceptos cardinales de los números intuitivos y las habilidades del reconocimiento verbal de los números  pueden servir como base, para una amplia variedad de números, cuentas y, conceptos y habilidades matemáticas. El reconocimiento intuitivo de los números puede ayudar literalmente a los niños y a las niñas a ver que un conjunto que tiene marca “dos” tiene más, que un conjunto que marca “uno” y que el conjunto que marca “tres”, tiene más objetos que el conjunto de nombre “dos”.  Esta comprensión ordinal básica de comprensión de los números, a su vez, puede ayudar a los niños y las niñas a reconocer la secuencia de las palabras de los números (uno, dos, tres…) y que representa colecciones cada vez más grandes. Cuando el niño o la niña se familiarizan con la secuencia del conteo, pueden desarrollar las habilidades para comenzar desde cualquier punto de secuencia del conteo y decir el siguiente número de la secuencia instantáneamente, en vez de contar desde “uno”.

La capacidad automática de nombrar un número después de otro, puede ser la base para la comprensión de que la adición de “uno” a un número resulte un número mayor, y más específicamente, la regla para después de la serie n+1/1+n hechos. Al añadir “uno”, la suma es el número después de otro número en la secuencia del conteo (por ejemplo, la suma de 7 + 1 es el número después de “siete” cuando contamos u “ocho”). Esta razonable estrategia puede hacer que los niños y las niñas sean capaces deducir de manera eficiente, la suma de cualquier combinación por la cual sepan la secuencia del conteo, incluso quienes no hayan practicado mayores múltiplos de dígitos, como 28 + 1, 128 + 1 o 1.000. En el tiempo, esta estrategia se convierte en un razonamiento automático y se puede aplicar eficientemente, sin deliberación (es decir, se convierte en un componente de la red de recuperación). En otras palabras, es la base para el acto de la fluidez  con los n+1/1+n combinaciones.

El reconocimiento verbal de los números y el concepto de los números cardinales, puede ser una base significativa de las cuentas.¹⁷ Los niños y las niñas que pueden reconocer los números “uno, dos y tres” tienen más posibilidades de beneficiarse de los esfuerzos de enseñanza de las personas adultas, para que aprendan a contar de quienes no pueden. Asimismo, pueden reconocer el propósito del recuento de objetos (como otra forma de determinar el conjunto total) y la racionalidad de los procedimientos para contar objetos (por ejemplo, la razón de por qué se enfatiza en repetir la última palabra del número utilizado en el conteo y  que representa el total contado). El objeto contado con sentido es necesario para la generación de estrategias de cuentas (con objetos o números de palabras) para determinar las sumas o las diferencias. A medida que estas estrategias se han vuelto eficientes, la atención se ha focalizado para descubrir patrones y relaciones, e incluso pueden servir como base para estrategias de relacionamiento (por ejemplo, usar los hechos y relaciones conocidas para deducir la respuesta de una combinación desconocida). También cuando estas estrategias de razonamiento se vuelven automáticas, logran ser utilizadas para producir respuestas eficientes desde la memoria o de la red de recuperación.

El reconocimiento verbal de los números puede permitir a un niño o a una niña ver uno – uno – uno como tres y al revés (por ejemplo, tres como uno- uno – uno). Lo que conlleva al niño o la niña construir una comprensión de la composición y la descomposición (en su conjunto puede ser construido y dividirse de las partes individuales, que a menudo tienen diferentes sentidos). Al ver repetidamente la composición y descomposición de dos o tres,  se puede conseguir la fluidez sencilla de la adición y la sustracción (por ejemplo, el conjunto de cuatro como “dos y dos” y escuchar a otra persona confirmar “sí, dos y dos son cuatro”) se pueden llevar a cabo fluidamente simples sumatorias hasta cinco y encontrar el camino para descubrir el número después de la regla para n+1/1+n combinaciones (discutido con anterioridad).

El concepto cardinal, del reconocimiento verbal de los números y los conceptos de composición y descomposición pueden en su conjunto ofrecer las bases, para la construcción del concepto de la adición y la substracción. Por ejemplo, para incluir un objeto a un conjunto de dos, un niño o una niña pueden ver literalmente que el conjunto se ha transformado a lo largo de un conjunto de tres. También, estas competencias pueden solventar los fundamentos para una construcción relativamente concreta e incluso abstracta al comprender la secuencia de los conceptos matemáticos¹⁸:

• El concepto de la negación de la sustracción. Por ejemplo, cuando los niños y las niñas reconocen que si se tienen dos bloques y quitas dos, no quedará nada, esto puede inducir a inducir al patrón que cualquier número se puede quitar y no dejar nada.
• El concepto de identificar la adición y la sustracción. Por ejemplo, cuando los niños y las niñas reconocen que dos bloques, cuando no se toman estos dos bloques, esto puede inducir a la regularidad, que si no se toman los números, el número no cambiará. Los conceptos de la negación y la identidad de la sustracción pueden proporcionar una base para la fluidez con n – n = 0 y n – 0 = n familias de operaciones de resta respectivamente.

Una debilidad del sentido numérico, es que puede interferir con el hecho de la fluidez y otros aspectos para el logro matemático . Por ejemplo, Mazzocco y Thompson¹⁹ encontraron que el rendimiento de los niños y las niñas preescolares, en cuatro objetos de la prueba de las habilidades matemáticas- segunda edición (TEMA -2) fue predictiva para detectar posibles dificultades en las matemáticas en segundo y tercer grado principalmente en el recuento de objetos (reconociendo que la última palabra del número contado indica el total), cardinalmente comparando los números de un dígito por ejemplo, ¿qué número es más: cinco o cuatro?) Adicionando mentalmente y leyendo números de un dígito. Nota: reconocer intuitivamente números verbales de un dígito es la base para las tres primeras habilidades  del aprendizaje y el paso principal para la cuarta.

Cuestión 4. Las bases para apoyar a los y las estudiantes a construir ambos sentidos numéricos y el hecho de la fluencia, en particular es para  generar oportunidades que puedan apoyar a descubrir patrones y relaciones. Por ejemplo. Un niño o una niña que ha aprendido que “los dobles”, tales como 5 + 5 = 10 y 6 + 6 = 12 es significativo (por ejemplo, cuando reconocen que en una suma son pares y se cuentan por dos números) este conocimiento se puede utilizar para razonar las sumas de dobles desconocidos, como 5 + 6 o 7 + 6.

Lo anterior, para que sea aprovechado apropiadamente como una oportunidad del aprendizaje, debiera tener un propósito significativo y una base de investigación.²⁰

• La instrucción debe tener un propósito y un encanto para los niños y las niñas. Lo que se puede lograr a través de la incorporación de la enseñanza del juego estructurado (por ejemplo, jugar un juego que consiste en lanzar un dedo, para que se reconozcan los patrones regulares del uno al seis). Las lecciones de arte y música pueden servir como vehículos naturales para pensar en los patrones, números y formas (por ejemplo,  manteniendo un ritmo de dos o tres, dibujando grupos de globos). Los padres y las madres y profesores(as) pueden aprovechar las diferentes situaciones cotidianas (por ejemplo, ¿cuántos pies tienes?... luego, ¿cuántos calcetines vas a tomar del cajón?) y demuestra que las preguntas de los niños y las niñas pueden ser importantes para enseñar con propósito.
• La instrucción debe ser significativa para los niños y las niñas para su construcción gradual progresiva (y realizar conexiones) ¿qué deberían saber? Una meta significativa para personas adultas que tienen que trabajar con niños y niñas de dos años, es que reconozcan el dos, para impulsarles a reconocer rápidamente números más grandes, como cuatro, pero puede ser abrumador y que se desalienten (implicando una falta de atención, reacciones de forma agresiva, comiencen a adivinar o retirarse de la actividad).
• La instrucción debe basarse en requerimientos o invitar a la reflexión en la medida de lo posible. Asimismo, se les debiera dar a los niños y a las niñas la oportunidad de pensar acerca un problema o tareas, para hacer conjeturas, diseñar sus propias estrategias o deducir sus propias respuestas.

Así varios de estos puntos son ilustrados a través del caso de Alicia²¹ y Lukas.²²

• El caso de Alicia. A los 2,5 años había sido capaz de reconocer durante meses uno, dos o tres objetos. Por lo que, su padre y madre querían ampliar el rango de los números a cuatro, aunque por su edad no estuviera dentro del rango de su competencia. Así en lugar de etiquetar simplemente conjuntos de cuatro, le empezaron a preguntar sobre colecciones de a cuatro. Generalmente, Alicia respondió por la descomposición irreconocible de dos conjuntos familiares de a dos, lo que llevó a que le preguntaran “dos y dos son cuatro. A los 30 meses, le mostraron una fotografía de cuatro cachorros, Alicia mostró dos dedos de su mano izquierda sobre dos perros y dijo “dos”. Al mismo tiempo, ella mostró dos dedos de su mano derecha y los colocó sobre los otros dos perros de la fotografía y dijo “dos”, entendiéndose que conocía la relación de “2 y 2 son 4 “, (lo había aprendido de su padre y madre) para especificar el valor cardinal de un conjunto.
• El caso de Lukas. En el contexto basado en un juego matemático en un computador, se le presentó a Lukas 6 + 6, quien determinó la suma contando. Luego se le presentó 7 + 7, él sonrió y rápidamente dijo “trece”, pero se le indicó que la suma era “catorce” y quedó desconcertado. Posteriormente, se le mostró 8 + 8  y señaló “iba a decir quince, porque 7 + 7 son 14, pero antes 6 + 6 era 12 y había pensado que 7 + 7 era 13, sólo que se me indicó que era 14, por eso ahora diré que es 16”.

Direcciones futuras

Aún queda mucho por aprender sobre el desarrollo matemático preescolar y quedan pendientes las siguientes preguntas ¿las habilidades del reconocimiento visual de los números a los dos años pueden preparar para la lectura en el jardín o el logro matemático en la escuela? Si es así, ¿la intervención se podría centrar en ejemplos y no ejemplos sobre la capacidad de medir el riesgo académico con sus pares?, ¿qué otros conceptos o habilidades a los dos o tres años pueden preparar la lectura en el jardín o el logro matemático en la escuela?, ¿qué tan eficaces son los programas de matemáticas en primera infancia, que se han desarrollado en la actualidad?

Conclusiones

Contrariamente a las creencias de personas educadoras de la temprana infancia, la enseñanza de las matemáticas para los niños y las niñas de tan sólo dos años pueden generar el sentido en esta materia.^23,24,25,26 Como lo muestra la Figura 1 que deja en claro, la enseñanza debiera comenzar enseñando a construir el concepto cardinal intuitivo de los números y la habilidad de reconocer y etiquetar conjuntos de uno a tres objetos con una apropiada palabra numérica. Además, como lo muestra la Figure 1 estos aspectos del aprendizaje de los números son la clave más tarde para las matemáticas y a menudo para detectar las tempranas discapacidades de los niños y las niñas con las matemáticas.²⁷ Lo que no significa imponer conocimientos en la etapa preescolar o hacerles memorizar hechos aritméticos, sino que fomentar el sentido numérico y el hecho de la fluidez, y que se deberían centrar en apoyar a los niños y a las niñas a descubrir relaciones y fomentar su intervención de estrategias de razonamiento.

Figura 1. Trayectoria de aprendizaje de conceptos y aptitudes claves en materia de números, de conteo y de aritmética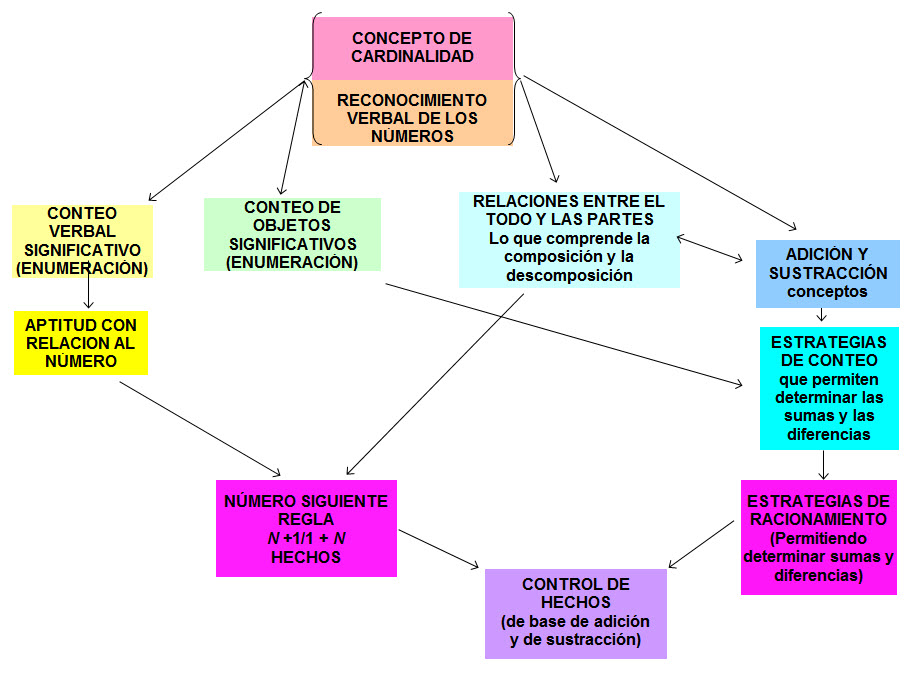

La investigación presentada fue apoyada en parte por la Fundación Nacional de Ciencias (BCS-0111829), la Fundación Spencer (Subvención 200400033), el Instituto Nacional de Salud (1 R01 HD051538-01), y el Instituto Nacional de Educación (R305K050082). Las opiniones expresadas en el siguiente manuscrito son exclusivas de su autor y no reflejan necesariamente la posición, la política o el respaldo de las instituciones mencionadas.

Referencias

1. Baroody AJ, Dowker A. The development of arithmetic concepts and skills:  Constructing adaptive expertise. In: Schoenfeld A, ed. Studies in mathematics thinking and learning series.  Mahwah, NJ: Lawrence Erlbaum Associates; 2003.
2. Kilpatrick J, Swafford J, Findell B, eds. Adding it up: Helping children learn mathematics. Washington, DC: National Academy Press; 2001.
3. Baroody AJ, Lai ML, Mix KS. The development of number and operation sense in early childhood. In: Saracho O, Spodek B, eds. Handbook of research on the education of young children. Mahwah, NJ: Erlbaum; 2006: 187-221.
4. Clements D, Sarama J, DiBiase AM, eds. Engaging young children in mathematics: Standards for early childhood mathematics education. Mahwah, NJ: Lawrence Erlbaum Associates; 2004: 149-172.
5. Ginsburg HP, Klein A, Starkey P. The development of children’s mathematical knowledge: Connecting research with practice. In: Sigel IE, Renninger KA, eds.  Child psychology in practice. 5th Ed. New York, NY: Wiley & Sons; 1998; 401–476. Handbook of child psychology, vol 4.
6. Baroody AJ. Why children have difficulties mastering the basic number facts and how to help them. Teaching Children Mathematics 2006;13:22–31.
7. Baroody AJ, Thompson B, Eiland M. Fostering the fact fluency of grade 1 at-risk children. Paper presented at: The annual meeting of the American Educational Research Association. April, 2008. New York, NY.
8. Gersten R, Chard, D. Number sense: Rethinking arithmetic instruction for students with mathematical disabilities. The Journal of Special Education 1999;33(1):18–28.
9. Jordan NC. The need for number sense. Educational Leadership 2007;65(2):63–66.
10. Dowker AD. Individual differences in arithmetic: Implications for psychology, neuroscience and education. Hove, England: Psychology Press; 2005.
11. Baroody AJ. The development of kindergartners' mental-addition strategies. Learning and Individual Differences 1992;4:215-235.
12. Baroody AJ, Eiland M, Thompson B. Fostering at-risk preschoolers' number sense. Early Education and Development 2009;20:80-120.
13. Mix KS, Sandhofer CM, Baroody AJ. Number words and number concepts: The interplay of verbal and nonverbal processes in early quantitative development. In: Kail R, ed. Advances in child development and behavior, vol 33. New York, NY: Academic Press; 2005: 305-346.
14. Baroody AJ, Li X, Lai ML. Toddlers’ spontaneous attention to number. Mathematics Thinking and Learning 2008;10:1-31.
15. Dehaene S. The number sense. New York, NY: Oxford University Press; 1997.
16. Wynn K. Numerical competence in infants. In; Donlan C, ed. Development of mathematical skills. Hove, England: Psychology Press; 1998: 1-25.
17. Benoit L, Lehalle H, Jouen F. Do young children acquire number words through subitizing or counting? Cognitive Development 2004;19:291–307.
18. Baroody AJ, Lai ML, Li X, Baroody AE. Preschoolers’ understanding of subtraction-related principles. Mathematics Thinking and Learning 2009;11:41–60.
19. Mazzocco M, Thompson R. Kindergarten predictors of math learning disability. Learning Disabilities Research & Practice 2005;20:142-155.
20. Baroody AJ, Coslick RT. Fostering children's mathematical power: An investigative approach to K-8 mathematics instruction. Mahwah, NJ: Erlbaum; 1998.
21. Baroody AJ, Rosu L. Adaptive expertise with basic addition and subtraction combinations: The number sense view. In: Baroody AJ, Torbeyns T. chairs. Developing Adaptive Expertise in Elementary School Arithmetic. Symposium conducted at: The annual meeting of the American Educational Research Association. April, 2006. San Francisco, CA.
22. Baroody AJ. Fostering early number sense. Keynote address at: The Banff International Conference on Behavioural Science. March, 2008. Banff, Alberta.
23. Baroody AJ, Li X. Mathematics instruction that makes sense for 2 to 5 year olds. In: Essa EA, Burnham MM, eds. Development and education: Research reviews from young children. New York: The National Association for the Education of Young Children; 2009: 119-135.
24. Bredekamp S, Copple C. Developmentally appropriate practice in early childhood programs.  Washington, DC:  National Association for the Education of Young Children; 1997.
25. Copley J, ed.  Mathematics in the early years, birth to five. Reston, VA: National Council of Teachers of Mathematics; 1999.
26. Copley J, ed. The young child and mathematics. Washington, DC: National Association for the Education of Young Children; 2000.
27. Landerl K, Bevan A, Butterworth B. Developmental dyscalculia and basic numerical capacities: A study of 8-9 year old students. Cognition 2004;93:99–125.